AeroDavid

Happy Fibonacci Day! The first four digits of the Fibonacci sequence, given by:

x_i=x_{i-1}+x_{i-2}, x_1=1,x_2=1

Form the date 11/23. However, this sequence is also useful in an application that surprised me a lot when I learned this earlier this year in my optimization class: one-dimensional line search methods.

Optimization in $\mathbb{R^n}$ often involves algorithms that are iterative in some way, that is, you start with a guess for the minimizer and iterate a certain computation until you arrive at the actual minimizer (or within acceptable tolerance). A big part of the study of these methods is to characterize their convergence rates, stability, etc.

However, despite these problems being in multiple dimensions, it is often the case that a one-dimensional optimization problem finds itself being a part of such iterative algorithms. This is the case for popular methods such as the steepest descent, or the conjugate gradient algorithm.

It is in these 1D, line-search methods that the Fibonacci Sequence pops up. In fact, another fun number pops up: the golden ratio! Let’s build up to it.

Section Search Methods

Consider a 1D, unimodal function, that is, the function has a single minimizer in the closed interval $[a_0, b_0]$ . Such a function is depicted below:

Unimodal function in [a0, b0] [1]

How could we find the minimizer effectively if we could evaluate the function at any x? That is, how could we be smart about picking where to evaluate the function in a way that leads us closer to the minimizer?

One such way is to recognize that we can try to narrow our range from $[a_0, b_0]$ to something smaller. We could try to pick some point in the interval and compare it to the value of the function at $a_0$ and $b_0$ . However, that wouldn’t tell us much: if the value is smaller than $a_0$ , it could just be the case that we overshot the minimizer. Likewise for comparisons to $b_0$ .

To narrow the range, therefore, we must evaluate the function at two different points. One way to go about this is to pick two points that are equally distant from their closest points, as shown in the figure below:

Section Search range reduction technique [1]

Where $a_1-a_0=b_0-b_1=\rho(b_0-a_0)$ with $\rho<1/2$ . We then evaluate the function at those new points. If $f(a_1)\geq f(b_1)$ , then the minimizer must be within $[a_1, b_0]$ . Otherwise, it must be within $[a_0,b_1]$ . An example of such range reduction is shown below:

Range reduction where f(a_1) < f(b_1) [1]

Golden Section Search

Now here’s a neat trick: to make this algorithm faster, it would be nice to minimize the number of times we have to evaluate the function $f(x)$ . Consider the case where $f(a_1)<f(b_1)$ as shown above. Note that we know the minimizer lies on the range $[a_0,b_1]$ and that $a_1$ already lies on that range. On top of that, we already evaluated $a_1$ ! Therefore, we can pick $a_1$ as the rightmost section endpoint for the next iteration, that is, $b_2=a_1$ . The range is reduced as follows:

Golden section search method [1]

We can write an expression for how fast this range is reduced. Note that:

b_1-b_2=\rho(b_1-a_0)

But $b_1-b_2=1-2\rho$ and $b_1-a_0=1-\rho$ . Therefore:

\rho(1-\rho)=1-2\rho

Which expands to the following quadratic expression for $\rho$ :

\rho^2-3\rho+1=0

Solving this for $\rho$ and demanding, as stated before, that $\rho<1/2$ gives:

\rho=\frac{3-\sqrt{5}}{2}

Some more manipulation yields the following observation:

\frac{\rho}{1-\rho}=\frac{1-\rho}{1}

Or dividing the range from $\rho$ to $1-\rho$ causes the ratio of the shorter to the longer segment to be equal to the ratio between the longer to the sum of the two. This is referred to as the golden ratio!

Fibonacci Search

Here comes Fibonacci: note that in the Golden Section search, we cut the range down by $\rho$ in every iteration, that is, the range reduction is fixed for every step. The following question arises: what if we allow this range reduction to vary from iteration to iteration?

Just like before, we would ideally only have to evaluate the function at a single new point at every iteration. Now, however, we allow ourselves to choose a different $\rho_k$ at every iteration. From the previous figure, we can conclude that the condition for $\rho_k$ to allow a single new evaluation at each iteration is:

\rho_{k+1}(1-\rho_k)=1-2\rho_k

Where any sequence $\{\rho_k\}=\rho_1,\rho_2,\rho_3...\rho_n$ that satisfies the condition above is valid. Rearranging leads to:

\rho_{k+1}=1-\frac{\rho_k}{1-\rho_{k}}

An example of a sequence that satisfies the condition above is the one chosen for the Golden Section Search, that is, $\rho_1=\rho_2=...=\rho_k=(3-\sqrt{5})/2$ .

After $N$ iterations, the range will be reduced by a factor of:

(1-\rho_1)(1-\rho_2)(1-\rho_3)...(1-\rho_N)=\prod_{k=1}^N(1-\rho_k)

So the question to be asked here is: how can choose the sequence $\{\rho_k\}=\rho_1,\rho_2,\rho_3...\rho_n$ so that we minimize this reduction factor $\prod_{k=1}^N(1-\rho_k)$ ? That is, how can we pick a sequence of cuts such that we cut the sequence by as much as possible at each iteration?

The proof for this is somewhat long, but it can be shown that such optimal sequence is of form:

\begin{matrix} \rho_1 = 1 - \frac{F_N}{F_{N+1}}\\ \\ \rho_2=1-\frac{F_{N-1}}{F_N} \end{matrix} \\ \\ \vdots \\ \rho_k=1-\frac{F_{N-k+1}}{F_{N-k+2}} \\ \vdots \\ \rho_N = 1 - \frac{F_1}{F_2}

Where $F_N$ is the $N$ th number of the Fibonacci Sequence! Note also that the range is reduced by a factor of $\frac{F_N}{F_{N+1}} \frac{F_{N-1}}{F_N}...\frac{F_1}{F_2}=\frac{F_1}{F_{N+1}}=\frac{1}{F_{N+1}}$ .

Example: minimizing $f(x)=x^2$

Let’s try this in Python.

Below is a snippet for a Fibonacci Search function:

def fibonacciSection(objective, interval, N, epsilon=0.05):
    F = [1, 1]
    for _ in range(2, N + 2):
        F.append(F[-1] + F[-2])

    intervals = []
    points = []

    left, right = interval
    lower = 'a'

    a = left + (F[N] / F[N + 1]) * (right - left)
    f_a = objective(a)
    b = left + (F[N - 1] / F[N + 1]) * (right - left)
    f_b = objective(b)

    for i in range(1, N + 1):
        if i != N:
            rho = 1 - F[N + 1 - i] / F[N + 2 - i]
        else:
            rho = 0.5 - epsilon

        if lower == 'a':
            b = a
            f_b = f_a
            a = left + rho * (right - left)
            f_a = objective(a)
        else:
            a = b
            f_a = f_b
            b = left + (1 - rho) * (right - left)
            f_b = objective(b)

        intervals.append((left, right))
        points.append((a, b))

        if f_a < f_b:
            right = b
            lower = 'a'
        else:
            left = a
            lower = 'b'

    return intervals, points

Which can be evaluated for any given objective function with an initial interval and number of iterations. Note that it is often the case that the number of iterations depends on some fixed tolerance. Since the interval reduction rate is known, the minimum number of iterations can be calculated. I am avoiding this for simplicity here.

Let’s run this for $f(x)=x^2$ . We call the function with:

objective = lambda x: x**2
interval = [-1, 1]
N = 20

intervals, points = fibonacciSection(objective, interval, N)

Plotting the interval length over the iterations, you can see the reduction in interval length as the algorithm narrows down to the region around [0, 0]:

Golden section search method [1]

Even more fun: we can animate this! Below is a GIF showing the algorithm at work:

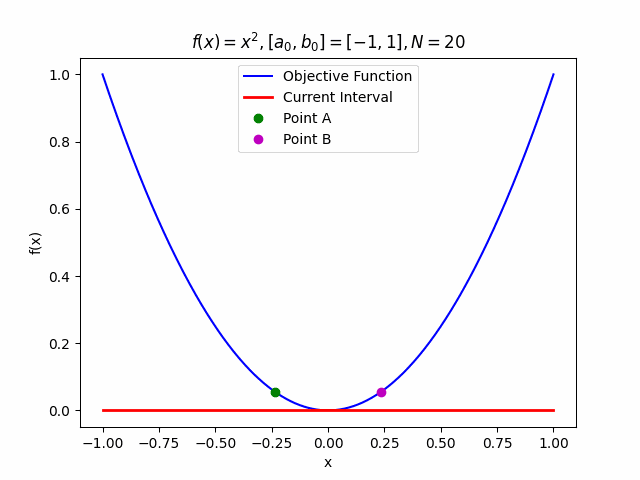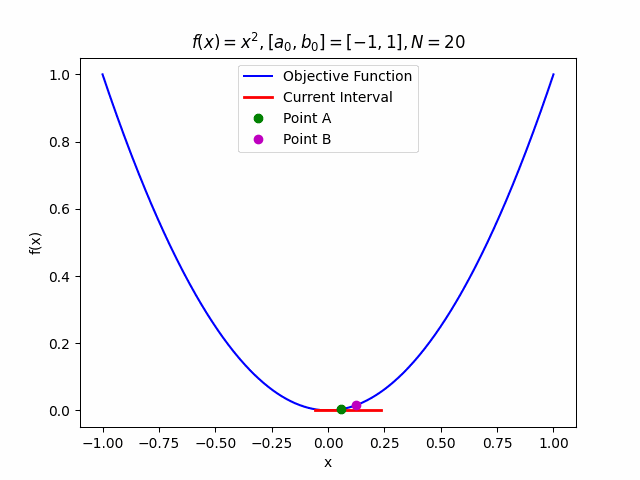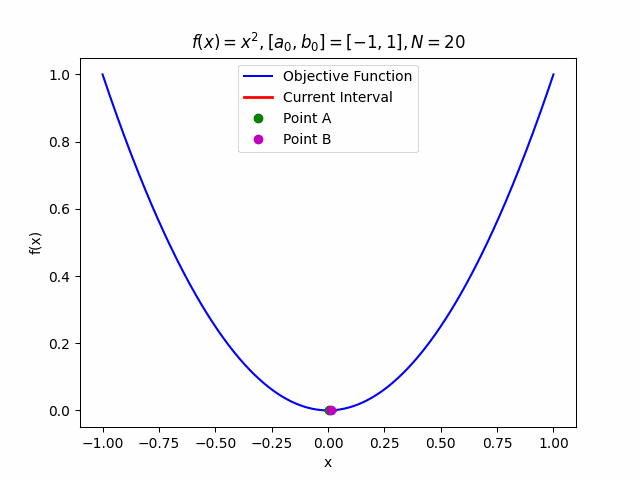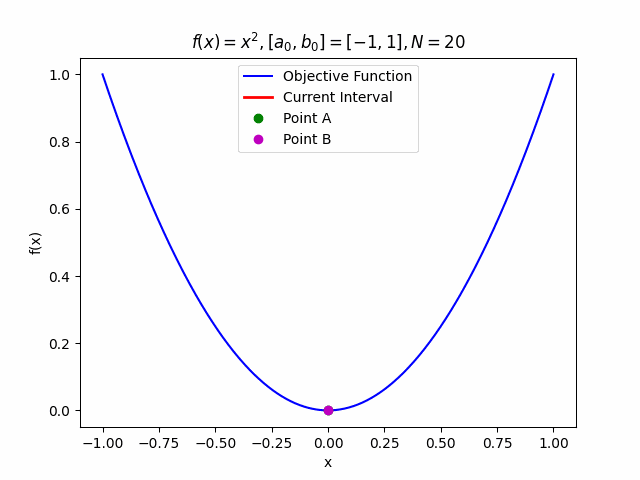
Conclusion

That’s about it for this post. This was a quick one for Fibonacci Day. Hopefully the GIF above works nicely. Will try to bring the topic back to aero next time. Woops!

Thanks for reading!

References